The Earned Schedule (ES) concept is very simple. It's a time magnitude or a time measurement. It's the instant of time in the plan which corresponds to the actual progress. If the project is behind schedule, ES will be the instant (in the past) at which the current progress should have been achieved. If the project is ahead of schedule, ES will be the instant (in the future) at which the current progress was planned to be achieved.
The way of finding the ES instant in time is the following. Find the instant in time distinct to the current instant in time (T) when the Planned Value (PV) was or will be equal to the current Earned Value (EV). Another way to see it is to project the Earned Value (EV) horizontally over the curve Planned Value (PV). It's explained in the following video.
Unfortunately, finding the Earned Schedule (ES) of a project would occasionally be a problem because of the discrete nature of the time series. This means that the Planned Value (PV) and the Earned Value (EV) are discrete values. Therefore, PV and EV are not continuous curves. For example: let the Planned Value at t1 be equal to 200. Let the Planned Value at t2 be equal to 250. It is possible that there is not an instant t when the Planned Value is exactly 230. In this example, if the Earned Value (EV) is 230, we will not find a pair of time instants t2 and t3 for which EV(t2) = PV(t3), excepting the origin. The example could be viewed in the following image.
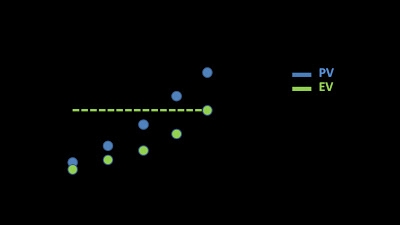
Theoretically the described problem doesn't exist. In theory, PV and EV have the same values or mathematically: they have the same range, because both are formed by the sum of the same increments that came from the same WBS, the same activities and the same measurement methods. Nevertheless, in practice, the measurement of EV and PV often have different range with disjointed discrete values. What can we do in this case?. The answer is simple: interpolate.
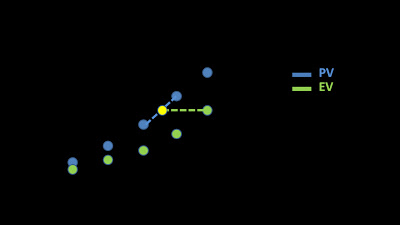
Supposing that `PV(t_1) <= EV(t)` and `PV(t_2) >= EV(t)`, then we can approximate:
`ES(t) = t_1 + (t_2 - t_1) * (EV(t) - PV(t_1))/(PV(t_2) - PV(t_1))`
This is a good and practical approximation to ES that I widely recommend.
