La Programación Ganada es un indicador de la Gestión de Valor Ganado (EVM). El concepto de Programación Ganada (ES) es muy simple, es una magnitud de tiempo o una medida en unidades de tiempo. Corresponde al instante de tiempo en que el progreso planeado es igual al progreso real (actual). Si el proyecto está retrasado, ES será un instante (en el pasado) en el que se debería haber logrado el progreso actual. Si el proyecto se adelanta a lo programado, ES será un instante (en el futuro) en el que se planificó el progreso actual.
La forma de encontrar ES instantánea en el tiempo es la siguiente. Encuentre el instante en el tiempo distinto al instante actual en el tiempo (T) cuando el valor planificado (PV) fue o será igual al valor ganado actual (EV). Otra forma de verlo es proyectar el Valor Ganado (EV) horizontalmente sobre el Valor Planificado (PV) de la curva.
Desafortunadamente, encontrar la Programación Ganada (ES) de un proyecto ocasionalmente podría ser un problema debido a la naturaleza discreta (no continua) de la serie de tiempo. Esto significa que el Valor planificado (PV) y el Valor ganado (EV) son valores discretos. Por lo tanto, PV y EV no son curvas continuas. Por ejemplo: supongamos que el valor planificado en t1 es igual a 200. Supongamos también que el valor planificado en t2 es igual a 250. Es posible que no haya un instante t cuando el valor planificado es exactamente 230. En este ejemplo, si el Valor Ganado (EV) es 230, no encontraremos un par de instantes de tiempo t3 y t4 para los cuales EV (t3) = PV (t4), excepto el origen. El ejemplo se puede ver en la siguiente imagen.
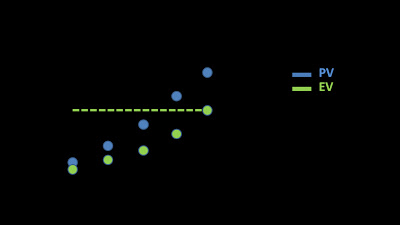
En teoría, el problema descrito no existe. En teoría, PV y EV tienen los mismos valores o matemáticamente: tienen el mismo rango, porque ambos están formados por la suma de los mismos incrementos que provienen de la misma WBS, las mismas actividades y los mismos métodos de medición. Sin embargo, en la práctica, la medición de EV y PV a menudo tienen un rango diferente con valores discretos inconexos. ¿Qué podemos hacer en este caso ?. La respuesta es simple: interpolar.
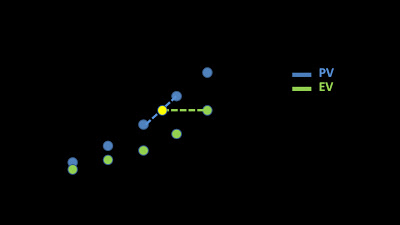
Suponiendo que `PV(t_1) <= EV(t)` and `PV(t_2) >= EV(t)`, podemos aproximar:
`ES(t) = t_1 + (t_2 - t_1) * (EV(t) - PV(t_1))/(PV(t_2) - PV(t_1))`
Esta es una buena y práctica aproximación a ES que recomendamos ampliamente.

